바로 프로젝트 적용 가능한 FIR Filter (low/high/band pass filter )를 c나 python으로 만들기

 band pass filter 코드가 필요해 인터넷을 검색을 해봤지만, 쓸 만한 코드와 자료가 별로 없어 그냥 만들어 쓰기로 했다.

필요한 공식은 위키피디아에 나와있다.

https://en.wikipedia.org/wiki/Finite_impulse_response


1. filter 크기

FIR filter를 만들 때 filter의 크기(tpas의 크기)를 결정할 때 도움될 수식이 있다.

  N=A㏈Fs / 22*Δf

A㏈ : 감쇄될 db
Fs : Sampling Frequency
Δf : frequency bandwidth

출처 : https://www.allaboutcircuits.com/technical-articles/design-of-fir-filters-design-octave-matlab/


def estimatefilterlen(fl,fh,fs,db):
    N = int(np.round(db * fs / (22 * (fh-fl)))-1)
    return N


2. Low Pass Filter

[ python code ]

def lowpassfilter(f,fs,N):
    taps = np.zeros(N)
    
    fc = f / fs
    omega = 2*np.pi*fc

    middle = int(N/2)
    for i in range(N):
        if i == middle:
            taps[i] = 2*fc
        else:
            taps[i] = np.sin(omega*(i-middle))/(np.pi*(i-middle))
        
    return taps


[ c code ]

#ifndef PI
#define PI 3.14159265358979323846
#endif

double *lowpassfilter(double f, double fs, int N)
{
    double *filter = NULL;
    double fc = 0;
    double omega = 0;
    int i = 0;
    int middle = 0;

    if (f <= 0 || fs <= 0 || N <= 0)
        return NULL;

    filter = (double*)malloc(N*sizeof(double));
    if (!filter)
        return NULL;

    memset(filter, 0, N*sizeof(double));

    middle = (int)(N / 2);
    fc = f / fs;
    omega = 2 * PI*fc;

    for (i = 0; i < N; i++)
    {
        if (i == middle)
        {
            filter[i] = 2 * fc;
        }
        else
        {
            filter[i] = sin(omega*(i - middle)) / (PI*(i - middle));
        }
    }
    return filter;
}


f = 2.0, fs = 100, N=908 인 low pass filter는 아래와 같은 모양과 주파수 응답 특성을 지닌다.


만약 위 1번의 필터 크기 결정 공식에 따라 필터의 크기를 달리 했을 경우의 예는 아래와 같다.



필터의 크기에 따라 주파수 응답 특성이 다르게 나타나는 것을 볼 수 있다. 필터의 길이가 길수록 주파수 응답 특성이 좋아지나 실시간 필터링의 경우 N/2 만큼의 딜레이가 발생하기 때문에 주의 깊게 사용해야 한다.


3. High Pass Filter

[ python code ]

def highpassfilter(f,fs,N):
    taps = np.zeros(N)
    
    fc = f / fs
    omega = 2*np.pi*fc
    
    middle = int(N/2)
    for i in range(N):
        if i == middle:
            taps[i] = 1 - 2*fc
        else:
            taps[i] = - np.sin(omega*(i-middle))/(np.pi*(i-middle))
                
    return taps


[ c code ]

double *highpassfilter(double f, double fs, int N)
{
    double *filter = NULL;
    double fc = 0;
    double omega = 0;
    int i = 0;
    int middle = 0;

   if (f <= 0 || fs <= 0 || N <= 0)
       return NULL;

    filter = (double*)malloc(N*sizeof(double));
    if (!filter)
        return NULL;

    memset(filter, 0, N*sizeof(double));

    middle = (int)(N / 2);
    fc = f / fs;
    omega = 2 * PI*fc;

    for (i = 0; i < N; i++)
    {
        if (i == middle)
        {
           filter[i] = 1 - 2 * fc;
        }
        else
        {
            filter[i] = - sin(omega*(i - middle)) / (PI*(i - middle));
        }
    }
    return filter;
}

f = 2.0, fs = 100, N=908 인 high pass filter는 아래와 같은 모양과 주파수 응답 특성을 지닌다.


4. Band Pass Filter

[ python code ]

def bandpassfilter(fl,fh,fs,N):
    taps = np.zeros(N)
    
    flc = fl/fs
    fhc = fh/fs
    omegal = 2*np.pi*flc
    omegah = 2*np.pi*fhc
    
    middle = int(N/2)
    for i in range(N):
        if i == middle:
            taps[i] = 2*fhc - 2*flc
        else:
            taps[i] = np.sin(omegah*(i-middle))/(np.pi*(i-middle)) - np.sin(omegal*(i-middle))/(np.pi*(i-middle))
    
    return taps


[ c code ]

double *bandpassfilter(double fl, double fh, double fs, int N)
{
    double *filter = NULL;
    double flc = 0;
    double omegal = 0;
    double fhc = 0;
    double omegah = 0;
    int i = 0;
    int middle = 0;

    if (fl <= 0 || fh <= 0 || fl >=fh || fs <= 0 || N <= 0)
        return NULL;

    filter = (double*)malloc(N*sizeof(double));
    if (!filter)
        return NULL;

    memset(filter, 0, N*sizeof(double));

    middle = (int)(N / 2);
    flc = fl / fs;
    omegal = 2 * PI*flc;
    fhc = fh / fs;
    omegah = 2 * PI*fhc;

    for (i = 0; i < N; i++)
    {
        if (i == middle)
        {
            filter[i] = 2*fhc - 2 * flc;
        }
        else
        {
            filter[i] = sin(omegah*(i - middle)) / (PI*(i - middle)) - sin(omegal*(i - middle)) / (PI*(i - middle));
        }
    }
    return filter;
}

fl = 1.0, fh = 2.0, fs = 100, N=908 인 band pass filter는 아래와 같은 모양과 주파수 응답 특성을 지닌다.


5. filtering

만들어진 FIR Filter를 사용하여 실제 샘플데이터를 필터링하는 코드는 아래와 같다. python코드가 간단해 python코드로 설명하겠다.

def filtering(samples, taps):
    N = taps.shape[0]
    out = np.zeros_like(samples)
    
    if len(samples) <= N:
        return out
        
    buffer = [samples[0] for _ in range(N)]
    buffer = np.hstack((buffer,samples))
    
    for i in range(len(samples)):
        out[i] = np.sum(buffer[i:i+N]*taps.T)
    
    return out[int(N/2):]



필터링은 convolution 연산을 사용한다. 필터의 길이에 해당하는 샘플과 필터의 합성곱의 결과들이 필터링 된 데이터가 된다. 연산을 위해 샘플 앞쪽에 필터의 길이만큼의 빈 데이터나 혹은 샘플의 끝부분 데이터 등을 넣어 추가해야 한다. 

필터링의 예제는 아래와 같다.

위와 같은 신호 데이터에 low pass filter를 적용하면 아래와 같은 결과를 얻을 수 있다.


6. windowing ***

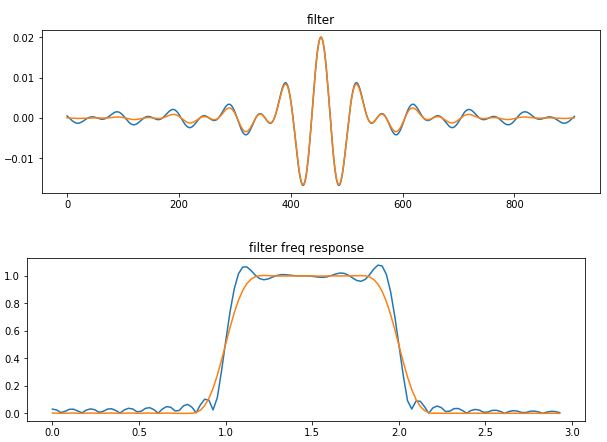
FIR Filter에 윈도우를 적용하면 주파수 특성이 좋아지는 것을 볼 수 있다. 아래는 Band Pass Filter에 Hamming 윈도우를 적용해 비교한 것이다. 

    bpf = bandpassfilter(fl=fl,fh=fh, fs=fs,N=N)
    bpfw = bandpassfilter(fl=fl,fh=fh, fs=fs,N=N)*np.hamming(N)

주파수 특성을 보면 잘라져 나가는 주파수 영역이 적용하지 전에 비해 깨끗해지는 것을 볼 수 있다. 

실제 샘플에 적용해 보면 아래와 같은 차이를 볼 수 있다.

위와 같이 단순 Band Pass Filter를 적용할 경우 저주파 영역에 주파수 성분이 나타나는 것을 볼 수 있으나, 아래처럼 hamming윈도우를 filter에 적용하여 필터링 할 경우 저주파 영역의 주파수 성분이 나타나지 않는다. 




관련 글

FFT용 윈도우 함수 구현 예제 소스 코드

댓글

  1. 익명2022년 3월 16일 오후 1:21

    글 잘보았습니다.
    혹시 filtering 코드를 c로 구현하려면 어떻게 해야할까요?

    답글삭제

댓글 쓰기

이 블로그의 인기 게시물

windows에서 간단하게 크롬캐스트(Chromecast)를 통해 윈도우 화면 미러링 방법

이미지
 Windows 10에서는 미라캐스트를 사용한 무선 디스플레이연결을 지원한다. 하지만, 만약 크롬캐스트(Chromecast)를 사용해 윈도우 화면을 미러링 하고자 할 때, 구글 크롬 브라우저를 사용하면 쉽고 편하게 할 수 있다. https://www.google.co.kr/intl/ko/chrome/ VLC에서도 비디오 화면을 미러링 할 수 있다고 하는데, 잘 동작하지 않고 윈도우 화면 전체를 미러링하지 않아 크롬 브라우저를 사용하고 있다. 크롬 캐스트 윈도우 화면 전송 방법 0. 크롬 캐스트 디바이스와 windows pc는 같은 네트웍에 연결되어 있어야 한다. (같은 공유기에 연결되어 있어야 한다.) 1. 크롬 브라우저의 우측 상단의 메뉴 > 전송을 클릭하면, 현재 사용가능한 크롬캐스트 디바이스 항목을 볼 수 있다. 2. 편의에 따라 탭 전송 아이콘에서 우측 버튼을 클릭하여 항상 표시되게 설정할 수도 있다. 3.  윈도우 화면 전체를 전송하고자 할 때는 탭 전송의 소스에서 '데스크톱 전송'을 선택하고, 바로 위의 크롬캐스트 디바이스를 클릭하면 된다. ** 소스는 미러링 중에는 변경되지 않는다. 먼저 소스를 선택하고 미러링해야 한다.  4. 화면 전송을 끝내고자 할 때는, 탭 전송에서 화면 전송중인 크롬캐스트 디바이스를 클릭하거나, 크롬 브라우저를 종료하면 된다.
자세한 내용 보기

간단한 cfar 알고리즘에 대해

이미지
Constant False Alarm Rate (CFAR)은 기본적으로 테스트하고자 하는 위치의 cell과 주변 cell의 관계를 보고 테스트 cell이 Target 인지 아닌지를 구분하는 알고리즘이다. 주변 cell과의 관계를 어떤 방식으로 비교하는가에 따라 여러가지 알고리즘이 존재한다. CA-CFAR, GO-CFAR, SO-CFAR, OS-CFAR, VI-CFAR, OSVI-CFAR등이 있다. 이 많은 알고리즘 중 간단하고 기본적인 CA-CFAR과 OS-CFAR에 대해 알아보자. CA-CFAR (Cell Average CFAR)   CA-CFAR의 원리는 위 그림과 같다. 좌우의 Reference Cell의 평균에 Scale Factor T를 곱하고, ADT (Average Decision Threshold)를 합하여 CUT가 타겟인지 아닌지를 구분한다. ADT는 신호의 white noise를 고려하기 위해 더해준다. Scale Factor T와 ADT는 아래와 같은 공식으로 사용할 수 있다. 사용하려는 시스템에 따라 공식은 달라질 수도 있다.   Pfa는 False Alarm 발생 확률을 나타내고, M과N는각 좌우의 Reference Cell의 개수를 나타낸다. OS-CFAR (Order Static CFAR)   OS-CFAR의 원리는 위 그림과 같다. 좌우의 reference cell중 K번째 큰 값의 cell을 Reference Cell의 대표 값으로 정해 CUT가 타겟인지 아닌지를 구분한다. 보통 전제 reference cell의 크기 순에서 (3*N)/4 번째 cell이 성능이 좋다고 알려져 있다. CFAR 사용 예 아래 사진은 위 두 cfar을 사용한 예다. 파란색은 신호이며, 붉은 색은 char을 사용해 만든 threshold이다. 이 threshold보다 큰 값의 신호가 있는 위치에 실제 Target이 있다고 볼 수 있
자세한 내용 보기

쉽게 설명한 파티클 필터(particle filter) 동작 원리와 예제

이미지
파티클 필터(particle filter)는 칼만 필터(kalman filter) 와 마찬가지로 노이즈가 있는 환경에서 측정된 데이터를 필터를 사용해 실제 위치를 추정하는 도구다. 파티클 필터(particle filter)는 보통 가우시안 분포가 아닌 측정 데이터를 다루기 위해 사용된다고 한다. 물론 가우시안 분포의 데이터에서 사용하지 말라는 건 아니다.  본 포스트에서는 파티클 필터(particle filter)의 어려운 수학적인 내용은 제하고, 쉽게 예를 들며 필터의 동작원리에 대해 알아보았다. 파티클 필터(particle filter)에 대해 검색해 보면 아래와 같은 그림을 많이 보게 된다. 아래 그림은 파티클 필터의 estimation cycle을 도식화한 것이다. <’Real-Time Tracking of Multiple Moving Objects Using Particle Filters and Probabilistic Data Association’ original scientific paper 中> 위 그림의 검은색 원들은 particle을 의미한다. 이 particle에는 보통 위치 데이터와 weight가 포함된다. 검은색 원이 큰 것이 있고 작은 것이 있는 이유는 weight가 크고 작음을 의마한다. typedef struct _particle_t {    int x;    int y;    float weight; }particle_t; 노이즈가 있는 환경에서 레이저 센서나 레이더등을 이용하여 물체의 위치를 측정할 때를 가정해 순서대로 이 필터가 동작하는 과정에 대해 알아 보겠다. (순서는 위 그림과 조금 다르다) 1. 초기 상태 측정 범위안에 랜덤 혹은 일정한 간경으로 particle을 뿌려 놓는다. 이 떄 particle의 weight는 모두 0으로 한다.   for(i
자세한 내용 보기

아두이노(arduino) 심박센서 (heart rate sensor) 심박수 측정 example code

이미지
하드 정리 중 예전에 만든 아두이노에서 심박센서를 사용하여 심박수 측정하는 소스 코드가 있어, 이를 블로그 글로 남긴다. 인터넷 쇼핑몰에서 쉽게 구할 수 있는 저렴함 센서가 사용 되었으며, 연결은 아래 그림과 같이 연결 되었다.      심박센서의 하트 부위에 손가락을 올려 놓고, 아날로그 A0값을 읽으면 심박의 움직임에 따라 A0값이 변하는 동작이 간단한 센서이다. 아래 그림의 왼쪽은 일정 시간 간격 마다 A0값을 읽어 시리얼 플로터로 본 심박에 따른 데이터이고, 오른쪽은 평균 필터를 사용해 노이즈를 제거한 후 시리얼 플로터로 본 데이터이다.   심박수는 수집된 데이터에서 threshold를 넘는 peak들의 시간 간격을 측정하여 계산한다.  peak위치를 찾는 방법은 여러 가지 방법이 있으나, 소스에 구현된 방법은 신호의 기울기가 +에서 0또는 -로 바뀌는 위치를 peak으로 선정하도록 하였다. 심장이 t시간동안 N회 뛰는 경우 심박수는 heart rate bpm = (N/t)*60 을 표현 할 수 있다.   threshold는 데이터를 보고 임의로 정했으며, 측정 데이터에 따라 자동으로 정하고 싶을 때는 cfar 같은 방법을 사용하면 된다.  소스는 아래와 같다. #define heartbit_adc_threshold      511 #define meanfilter_size             5 #define heartbit_tick_buffer_size   10 #define measure_buffer_size       3 float meanfilter[meanfilter_size] = {0,};
자세한 내용 보기